|
|
|
|||||||
في حال وجود أي مواضيع أو ردود
مُخالفة من قبل الأعضاء، يُرجى الإبلاغ عنها فورًا باستخدام أيقونة
( تقرير عن مشاركة سيئة )، و الموجودة أسفل كل مشاركة .
| آخر المواضيع |
|
بكالوريا تجريبي رياضيات رائع *أفكار جديدة و مميزة*
|
|
أدوات الموضوع | انواع عرض الموضوع |
2011-05-30, 23:10
|
رقم المشاركة : 1 | ||||
|
بكالوريا تجريبي رياضيات رائع *أفكار جديدة و مميزة*
بسم الله الرحمان الرحيم تفضلوا اخوتي هو بكالوريا تجريبي في الرياضيات من صنع أستاذي زواوي بارك الله فيه 100/100 فيه أفكار مميزة و جديدة مثل مجموعة النقط في الهندسة الفضائية: *مستوي يشمل نقطة g و عمودي على المستقيم AB كذلك الدالة يوجد فيها مناقشة بيانية للوسيط m لكن تحتاج للقيل من الذكاء و الدقة في الملاحظة لأنها غير واضحة للوهلة الأولى و الموضوع الثاني فيه أفكار أيضا في المتتالية :أولا شكلها و ثانيا برهان يعتمد على برهان بالتراجع أتمنى أن تحاولوا فيه و باذن الله سينال رضاكم انتظر أراءكم المفيدة https://up.djelfa.info/uploads/13067783701.jpg  https://up.djelfa.info/uploads/13067783702.jpg  https://up.djelfa.info/uploads/13067783703.jpg  ملاحظة تمرين الهندسة عوض النقطة I النقطة H https://up.djelfa.info/uploads/13067783704.jpg  تفضلوا الحل https://up.djelfa.info/uploads/13068600151.jpg  https://up.djelfa.info/uploads/13068600152.jpg  https://up.djelfa.info/uploads/13068600153.jpg  https://up.djelfa.info/uploads/13068600154.jpg 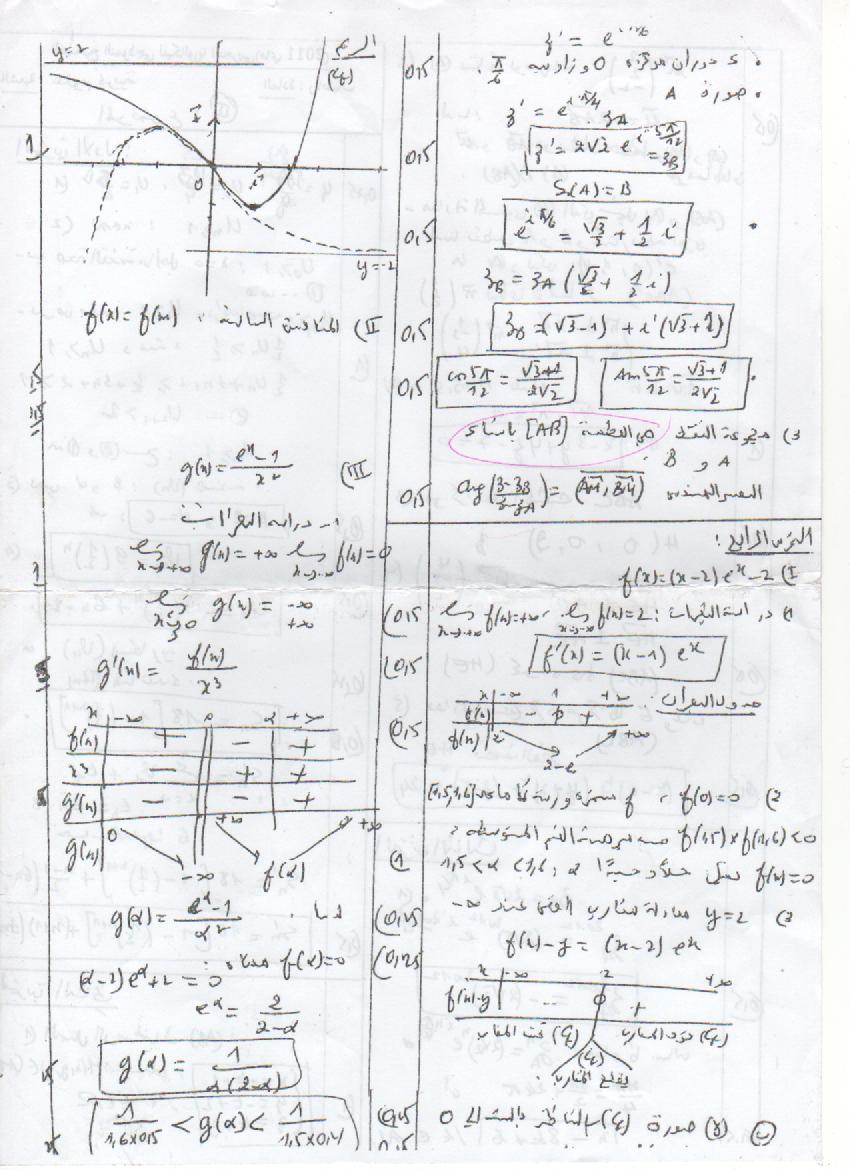 تفضلوا المناقشة البيانية https://up.djelfa.info/uploads/13069679871.jpg  هذا شرح بسيط للمناقشة https://up.djelfa.info/uploads/13069667241.jpg 
|
||||
|
2011-05-31, 10:01
|
رقم المشاركة : 3 | |||
|
موضوع رائع اظنه الاحسن الى حد الأن ارجو وضع التصحيح النموذجي |
|||
|
2011-05-31, 10:06
|
رقم المشاركة : 4 | |||
|
جزاك الله خيرا اخيتي |
|||
|
2011-05-31, 10:11
|
رقم المشاركة : 5 | |||
|
merci beaucoup |
|||
|
2011-05-31, 11:07
|
رقم المشاركة : 7 | |||
|
الى الاخت نسمة |
|||
|
2011-05-31, 11:12
|
رقم المشاركة : 9 | ||||
|
|
||||
|
2011-05-31, 11:26
|
رقم المشاركة : 10 | ||||
|
اقتباس:
بخصوص الاستنتاج عند حساب Sn نجد ((Sn = 2(1- (1/2)^(n-1 وبالتعويض ب عبارة Vn نجد Sn= Un - 1 (لأن كل حد يختزل بالذي بعده حتى نجد Sn= Un - U1) وبه تصبح (Un= 1 - (1/2)^(n-1 ثم نحسب نهاية Un اما تؤول الى زائد مالانهاية وبهاذا نتأكد من السؤال الثاني اظن انها الطريقة الصحيحة ارجو الا اكون اخطات في الحساب |
||||
|
2011-05-31, 11:33
|
رقم المشاركة : 12 | ||||
|
|
||||
|
2011-05-31, 11:38
|
رقم المشاركة : 13 | ||||
|
اقتباس:
بخصوص المجموع Sn من V1 الى V n-1 فيبقى لنا U1 و Un+1-1 وهو Un |
||||
|
2011-05-31, 11:42
|
رقم المشاركة : 14 | ||||
|
|
||||
|
2011-05-31, 11:45
|
رقم المشاركة : 15 | |||
|
لكن اذا طبقنا العبارة نجد Lim Un=1 |
|||
| الكلمات الدلالية (Tags) |
| رياضيات |
|
|
المشاركات المنشورة تعبر عن وجهة نظر صاحبها فقط، ولا تُعبّر بأي شكل من الأشكال عن وجهة نظر إدارة المنتدى
المنتدى غير مسؤول عن أي إتفاق تجاري بين الأعضاء... فعلى الجميع تحمّل المسؤولية
Powered by vBulletin .Copyright آ© 2018 vBulletin Solutions, Inc
العرض العادي
