

|
|
|||||||
في حال وجود أي مواضيع أو ردود
مُخالفة من قبل الأعضاء، يُرجى الإبلاغ عنها فورًا باستخدام أيقونة
![]() ( تقرير عن مشاركة سيئة )، و الموجودة أسفل كل مشاركة .
( تقرير عن مشاركة سيئة )، و الموجودة أسفل كل مشاركة .
| آخر المواضيع |
|
 |
|
|
أدوات الموضوع | انواع عرض الموضوع |
|
|
رقم المشاركة : 1 | ||||
|
la theorie de gauss seidel introduction La méthode de Gauss-Seidel est une méthode itérative de résolution d'un système linéaire (de dimension finie) de la forme 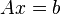 , ce qui signifie qu'elle génère une suite qui converge vers une solution de cette équation, lorsque celle-ci en a une et lorsque des conditions de convergence sont satisfaites (par exemple lorsque , ce qui signifie qu'elle génère une suite qui converge vers une solution de cette équation, lorsque celle-ci en a une et lorsque des conditions de convergence sont satisfaites (par exemple lorsque  est symétrique définie positive). L'algorithme suppose que la diagonale de est symétrique définie positive). L'algorithme suppose que la diagonale de  est formée d'éléments non nuls. est formée d'éléments non nuls.La méthode se décline en une version « par blocs ». Le principe de la méthode peut s'étendre à la résolution de systèmes d'équations non linéaires et à l'optimisation, mais avec des conditions d'efficacité moins claires. En optimisation, l'utilité de cette approche dépendra beaucoup de la structure du problème. Le principe gauss-seidelien permet aussi d'interpréter d'autres algorithmes. L'algorithme Principe Soit 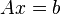 le système linéaire à résoudre, que l'on suppose écrit sous forme matricielle avec  et et  , ce qui signifie que l'on cherche , ce qui signifie que l'on cherche 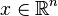 tel que le produit matriciel tel que le produit matriciel  soit égal à soit égal à  . .On note 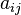 les éléments de les éléments de  et et  ceux de ceux de  : : La méthode de Gauss-Seidel résout le système linéaire 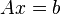 de manière itérative, ce qui veut dire qu'elle génère une suite de vecteurs de manière itérative, ce qui veut dire qu'elle génère une suite de vecteurs  , pour , pour  . On interrompt le calcul de la suite lorsque l'itéré courant, disons . On interrompt le calcul de la suite lorsque l'itéré courant, disons  , est jugé suffisamment proche d'une solution, par exemple parce que le résidu , est jugé suffisamment proche d'une solution, par exemple parce que le résidu  est petit. est petit.Soit  l'itéré courant. L'itéré suivant l'itéré courant. L'itéré suivant  se calcule en se calcule en  étapes, comme suit. étapes, comme suit.
 soient non nuls, on calcule les composantes soient non nuls, on calcule les composantes  de de  de manière séquentielle pour de manière séquentielle pour 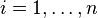 par par La formule fait intervenir les éléments  ( ( ) calculés dans les étapes précédentes ) calculés dans les étapes précédentes. L'expression matricielle de l'algorithme suppose que la matrice Convergence se décompose comme suit se décompose comme suit où  est la partie diagonale de est la partie diagonale de  , ,  (pour lower) sa partie triangulaire inférieure stricte et (pour lower) sa partie triangulaire inférieure stricte et  (pour upper) sa partie triangulaire supérieure stricte. (pour upper) sa partie triangulaire supérieure stricte.Une itération de la méthode de Gauss-Seidel, celle passant de  à à  , consiste alors à résoudre le système triangulaire inférieur , consiste alors à résoudre le système triangulaire inférieur de « haut en bas », c'est-à-dire en déterminant successivement  , ,  , ..., , ...,  . .La formule de mise à jour des itérés dans la méthode de Gauss-Seildel montre que ceux-ci sont des approximations successives pour le calcul d'un point fixe de l'application Erreur▲ Les propriétés de convergence de la méthode vont donc dépendre du spectre de la matrice  . .On sait que la méthode de Gauss-Seidel converge, quels que soient le vecteur  et le point initial et le point initial  , dans les situations suivantes : , dans les situations suivantes :
A chaque itération, le vecteur trouvé x(k+1) comporte une certaine erreur : Algorithme▲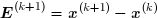 On pose P = D +L -1U . Il vient alors : On pose P = D +L -1U . Il vient alors :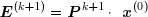
) Methode de gauss seidel dans Matlab ;L'algorithme et le programme de methode de gauss seidel dans Matlab; : Un vecteur initial x(0) étant donné, l'algorithme suivant permet de déterminer les éléments successifs de la suite. On décompose la matrice A en trois matrices L , D et U . La matrice L est constituée des termes qui se trouvent au-dessous de la diagonale principale de A(j < i) ; la matrice D contient les termes diagonaux de A(j = i) ; la matrice U est constituée des termes qui se trouvent au-dessus de la diagonale principale de A(j > i) . 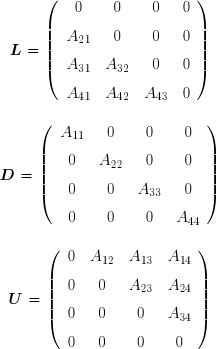 Le système à résoudre peut alors s'écrire : 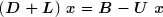 d'où l'on tire la formule de récurrence : 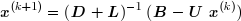 qui permet de calculer les composantes de x(k+1) lorsque celles de x sont connues : 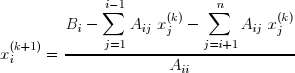 On remarquera que chaque composante de x(k) n'est utilisée que jusqu'au calcul de la composante correspondante de x(k+1) . Ces deux vecteurs peuvent donc être stockés dans le même tableau. le programme function gauss_seidel(A, b, N) Gauss_seidel (A, b, N) résoudre itérativement un système d'équations linéaires de sorte que A est la matrice de coefficients, et b est le vecteur colonne de droite. N est le nombre maximum d'itérations Le procédé mis en oeuvre est le Gauss-Seidel itératif. Le vecteur de départ est le vecteur nul, mais peut être ajustée à ses besoins. La forme itérative est basée sur la matrice de transition / itération de Gauss-Seidel Tg = inv (DL) * U et les constantes vecteur cg = inv (DL) * b. La sortie est le vecteur solution x . Ce fichier suit les directives données algorithmiques dans le livre https://m2matlabdb.ma.tum.de/gauss_seidel.m?MP_ID=406
|
||||

|
|
|
رقم المشاركة : 2 | |||
|
شكراا |
|||

|
|
|
رقم المشاركة : 3 | |||
|
شكرا جزيلا |
|||

|
|
|
رقم المشاركة : 4 | |||
|
le programme dans matlab avec un example- |
|||

|
 |
| الكلمات الدلالية (Tags) |
| gauss, seidellllll |
|
|
المشاركات المنشورة تعبر عن وجهة نظر صاحبها فقط، ولا تُعبّر بأي شكل من الأشكال عن وجهة نظر إدارة المنتدى
المنتدى غير مسؤول عن أي إتفاق تجاري بين الأعضاء... فعلى الجميع تحمّل المسؤولية
Powered by vBulletin .Copyright آ© 2018 vBulletin Solutions, Inc