درس حول الدوال المرجعية لكل من يريد

ميرة أنوشة · 2013-12-29, 19:30

أهلا وسهلا بكم
سنتناول في هذا درس كل مايتعلق بالدالة مربع

الدالة مربع من الشكل f(x)=x²

مجموعة التعريف
]∞+.∞-[=df

دراسة إتجاه تغير الدالة
في دراسة إتجاه تغير دالة ننطلق من شكل بسيط وأولي x1<x2 ونقوم إما بإضافة أو طرح أو ضرب ....وهذا حتى نتوصل لعبارة دالة (f(x بحيث أن إتجاه المتباينة يتغير بتطبيق خواص الحصر

إذا وجدنا في الأخير (f(x1)<f(x2 نقول عن الدالة أنها متزايدة
إذا وجدنا في الأخير (f(x1)>f(x2 نقول عن الدالة أنها متناقصة

ملاحظة:
تذكر أن الدالة مربع متزايدة على مجال ومتناقصة على مجال وهذا راجع للتربيع حيث عندما نربع أعداد موجبة لايتغير إتجاه المتباينة وعندما نربع أعداد سالبة يتغير إتجاه المتباينة ولهذا يجب أن نحدد مجالين مجال موجب ومجال سالب

نفرض أن x1<x2 بتربيع طرفي المتبانة نجد

أ) على المجال ]∞+.0] نجد :

x1²<x2² ومنه
(f(x1)<f(x2
إذن الدالة f متزايدة على المجال ]∞+.0]
ب)على المجال [0.∞-[ نجد:
x1²>x2² لاحظ أن إتجاه المتباينة قد تغير

(f(x1)>f(x2
إذن الدالة f متناقصة على المجال [0.∞-[

ملاحظة:
لاتكون المجالات الموجبة والسالبة دائما ثابة فهي تتغير بتغير العبارة

جدول التغيرات
هو جدول يبين تزايد وتناقص الدالة وهو مرتبط ب إتجاه تغير الدالة سيتم إعداد شرح مفصل له في الدروس القادمة

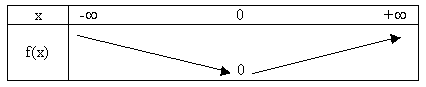
لاحظ أن الجدول يجسد إتجاه تغير الدالة فمن 0.∞- نلاحظ أن الدالة متناقصة ومن ∞+.0 نلاحظ أن الدالة متزايدة
التمثيل البياني للدالة
التمثيل البياني للدالة مربع عبارة عن فرع قطع مكافئ

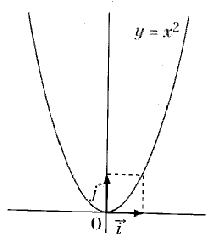
كما تلاحظ فالدالة زوجية فمنحناها البياني متناظر بالنسبة لمحور التراتيب ومنه نستنتج أن

(f(x)=f(-x
التحقيق
لدينا (f(x)=(x²
f(5)=5²
f(-5)=-5²=25
كما نعلم فاعند تربيع أي عدد سالب نتحصل على عدد موجب

2مجموعة تعريف الدالة
مجموعة التعريف هي كل القيم التي يمكن أن يأخذها العدد x دون أن يحدث تناقض في الدالة
التناقضات الموجودة
كسر مقامه يساوي الصفر
عدد سالب داخل الجذر

من هذه التناقضات يمكننا أن نستنتج مجموعة تعريف أي دالة وسأشرح مجموعة تعريف ثلاث دوال

الدالة مربع
من الشكل ƒ(x)=x²
في هذه الدالة يكننا أن نعوض x بأي قيمة دون أن يحدث أي تناقض في الدالة حيث أن الدالة لاتحوي لاكسر يحتوي على مقام به x ولا جذر ومنه نستنتج أن مجموعة التعريف هي
]∞ ,∞-[ المجال مفتوح عند الطرفين فلا يمكن أن نضع مجال مغلق لزائد أو ناقص مالا نهاية بل نتركه مفتوح

الدالة مقلوب
من الشكل ƒ(x)=1/x
في هذه الدالة يمكننا أن نعوض x بجميع القيم إلا الصفر حيث أن المقام لايجب أن يكون مساوي للصفر ومن هذا نستنتج أن مجموعة التعريف هي
]∞+ ,0[ إتحاد ]0.-∞[
ملاحظة سبب فتحنا للمجال عند الصفر هو عدم إنتماء الصفر إلى مجموعة التعريف بينما يمكننا وضع أي قيمة أخرى حتى ولو كانت 0.1 المهم لايكون المقام مساوي للصفر

ملاحظة:
قد يكون x مرفوق ب عدد أخر مثلا ƒ(x)=2/x+1 سأضع لكم طريقتين الأولى خاطئة والثانية صحيحة حتى يسهل الفهم

تحذير:
الحل الأول
تكون الدالة f معرفة إذا وفقط إذا كانت
x≠0
ومنه نستنتج أن مجموعة التعريف هي
]∞+ ,0[ إتحاد ]0.-∞[=df
خطأ

التصحيح

تكون الدالة f معرفة إذا وفقط إذا كانت
x+1≠0
x≠-1
ومنه نستنتج أن مجموعة التعريف

]∞+ ,1-[ إتحاد ]1-.∞-[ =df

خلاصة القول
يجب أن يكون المقام ككل غير مساوي للصفر وليس x فقط

الدالة جذرية أو الصماء

من الشكل (ƒ(x=جذر x
في هذه الدالة يمكننا التعويض بجميع القيم الأكبر والمساوية للصفر حيث لايمكن التعويض بعدد سالب ومنه نستنج أن مجموعة التعريف
0≤x

]∞+.0]=df

نفس الملاحظة الخاصة بالدالة مقلوب حيث أنه يجب أن يكون مابداخل الجذر ككل أكبر أومساوي للصفر وليس x فقط

إلى هنا نصل وإياكم إلى نهاية الدرس
والسلام خير الختام