slt pleaaaase ana na9era 2eme annè mo3adala fel math

[ilyas.65]

F(x)= (x+1)(x-4)
F(x)=(x-3/2)²-25/4

تحقق من هذا أخي أو أختي
الطريقة هي بنشر المعادلة الثانية حتى نصل الى المعادلة الأولى أرجوا منك طريقة النشر

[linalou]

أختي العزيزة
لدينا المعادلة الأولى :نشرها يساوي (x+1)(x-4)=x2-3x-4
و المعادلة الثانية F(x)=(x-3/2)2-25/4 =x2-3x-4
ومنه المعادلة الاولى=المعادلة الثانية
ملاحظة :x2 اقصد بها xمربع

[sari13]

بعدما تنشر المعادلة الأولى استعمل الشكل النموذجي للمعادلة من الدرجة 2
'شوف الشكل النموذجي في الكتاب)
توصل للحل مباشرة هكذا

[~ فآيـزة ~]

f(x)= (x-3/2)²-25/2
x² +9/4 - 3x - 25/4 =
x² - 4 -3x =
x² -3x -4 =

نحل هذه المعادلة عن طريق المميز (دلتا) فنجد حلين:
x= -1
x= 4

الآن نستعمل القسمة الاقليدية :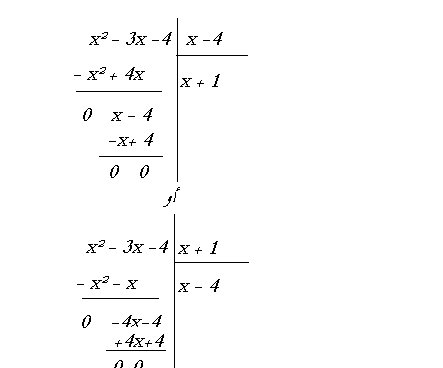



أي:
(f(x)= (x-3/2)²-25/2 = x² -3x -4 = (x+1)(x-4


ملاحظة: الحالة العامة للتحليل:
لتكن : f(x) = ax² + bx + c

ليكن حلاها: x1 و x2 : يكون التحليل:

(f(x) = a(x-x1) (x-x2

[ilyas.65]

thhhhhhhhhhhhhhx bq

[Abdelmalek Meziane]

المعادلة الأولى عبارة عن متطابقة شهيرة:
F(x)=(x-3/2)²- (5/2)²
ننشر هذه العبارة فنجد :
F(x)=(x-3/2)²- (5/2)²= (x-3/2+5/2) (x-3/2-5/2

(x-2/2)-(x-8/2)=(x-1)(x-4) =