ربما فهمت بعض ماتقولين
دالة القيمة المطلقة مثلها مثل باقي الدوال (تخضع لنفس القوانين) عند تحديد مجالها
لو نحكم على على الدالة انها معرفة على r هل سنكون محقين؟
مثلا يكون مابين رمز القيمة المطلقة عبارة عن كسر هل سنقول انها معرفة على r؟
الجواب هو لايمكننا الحكم حتى نرى مايوجد في المقام. لانه قد يكون مساويا للصفر عند قيمة ما
نعطي مثال

يطلب تعيين مجال تعريفها
الان ماعليك سوى توجيه نظرك الى المقام ومعرفة متى يكون مساويا للصفر اي
x-1=0 اي x=1 الان عندما يكون x يساوي 1 المقام يكون 0 ادا فهي غير معرفة عند 1(غير متصلة)
ادا فمجال تعريفها هو {r-{1
الان الى مثال 2
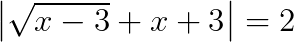
يجب على تفكيرك لاينصب على رمزي القيمة المطلقة بل يجب ان ينصب مايوجد في الداخل
نجد شيئا هو رمز الجذر . الان ماهو مجال تعريف الدالة جذر في r؟ هي معرف فقط في المجال الموجب من r.
اي ماتحت الجذر الموجب يجب ان يكون
x-3 ≥0 يعني ان ان x≥3
لدينا باقي مايوجد في الدالة لايهمنا .
مجال تعريف الدالة اذاا هو
]∞+;3]
الخلاصة هي عند
تعيين مجال تعريف دالة تحتوي على رمز القيمة المطلقة يهمنا مايوجد بين رمزيها .
ارجو ان الفكرة وصلت